Previous: SnappyHexMesh mesh Up: SnappyHexMesh mesh Next: castellatedMeshControls
This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.
Geometry
This block holds definition of input geometry (surfaces).
- Each surface can be used to:
- specify refinement for any mesh cell which:
- intersects the surface
- lies inside of a (closed) surface
- lies outside of a (closed) surface
- lies near a surface
- define the boundary and snap the mesh to the surface.
- specify refinement for any mesh cell which:
- Besides the input surface, user can directly define following objects:
- searchableBox
myBox { type searchableBox; min (-1.0 -0.7 0.0); max ( 8.0 0.7 2.5); } - searchableCylinder
myCylinder { type searchableCylinder; point1 (1 0 0); point2 (2 0 0); radius 0.1;myDisk { type searchableDisk; origin (0 0.5 0); normal (1 0 0); radius 0.01; } - searchablePlane
myPlane1 { type searchablePlane; planeType pointAndNormal; pointAndNormalDict { basePoint (0 0 0); normalVector (1 0 0); } }myPlane2 { type searchablePlane; planeType embeddedPoints; embeddedPointsDict { point1 (0 0 0); point2 (1 0 0); point3 (0 1 0); } } - searchablePlate
myPlate { type searchablePlate; origin (0 0 0); span (1 1 0); } - searchableSphere
mySphere { type searchableSphere; centre (0 0 0); radius 0.1; }
- searchableBox
- Each input geometry is defined as a block starting with the name of the file (inside the triSurface directory) and including:
- type triSurfaceMesh; – always the same for all input files
- name patchName; – user defined name to be used for referring to the input geometry
- The geometry block can contain any number of geometry parts or implicit objects:
geometry { C-fine.stl { type triSurfaceMesh; name C; } F-fine.stl { type triSurfaceMesh; name F; } D-fine.stl { type triSurfaceMesh; name D; } disk { type searchableDisk; origin (0.6925 0.5 0); normal (7 -2 0); radius 0.1; } }







![Node125 19 [*]](https://www.cfdsupport.com/wp-content/uploads/2022/02/crossref.png)
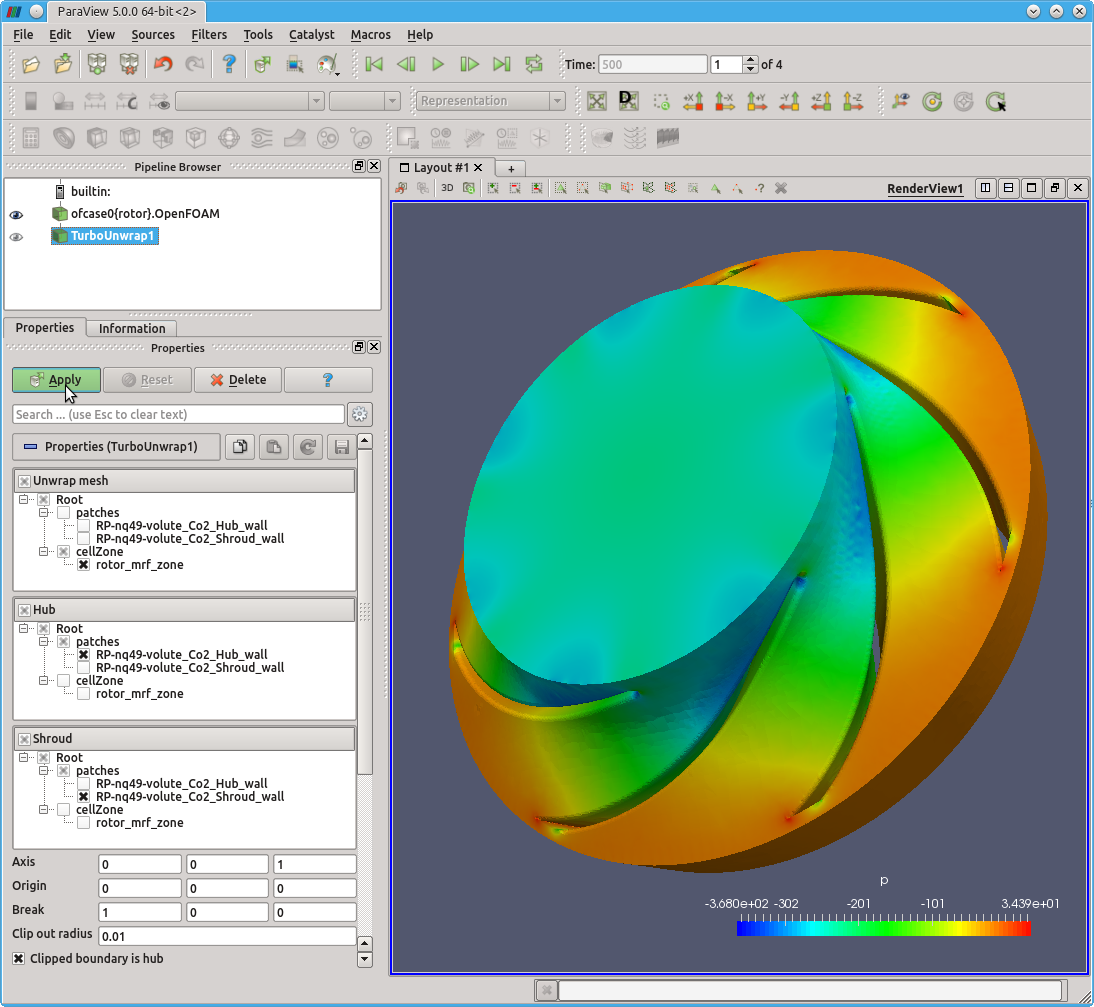
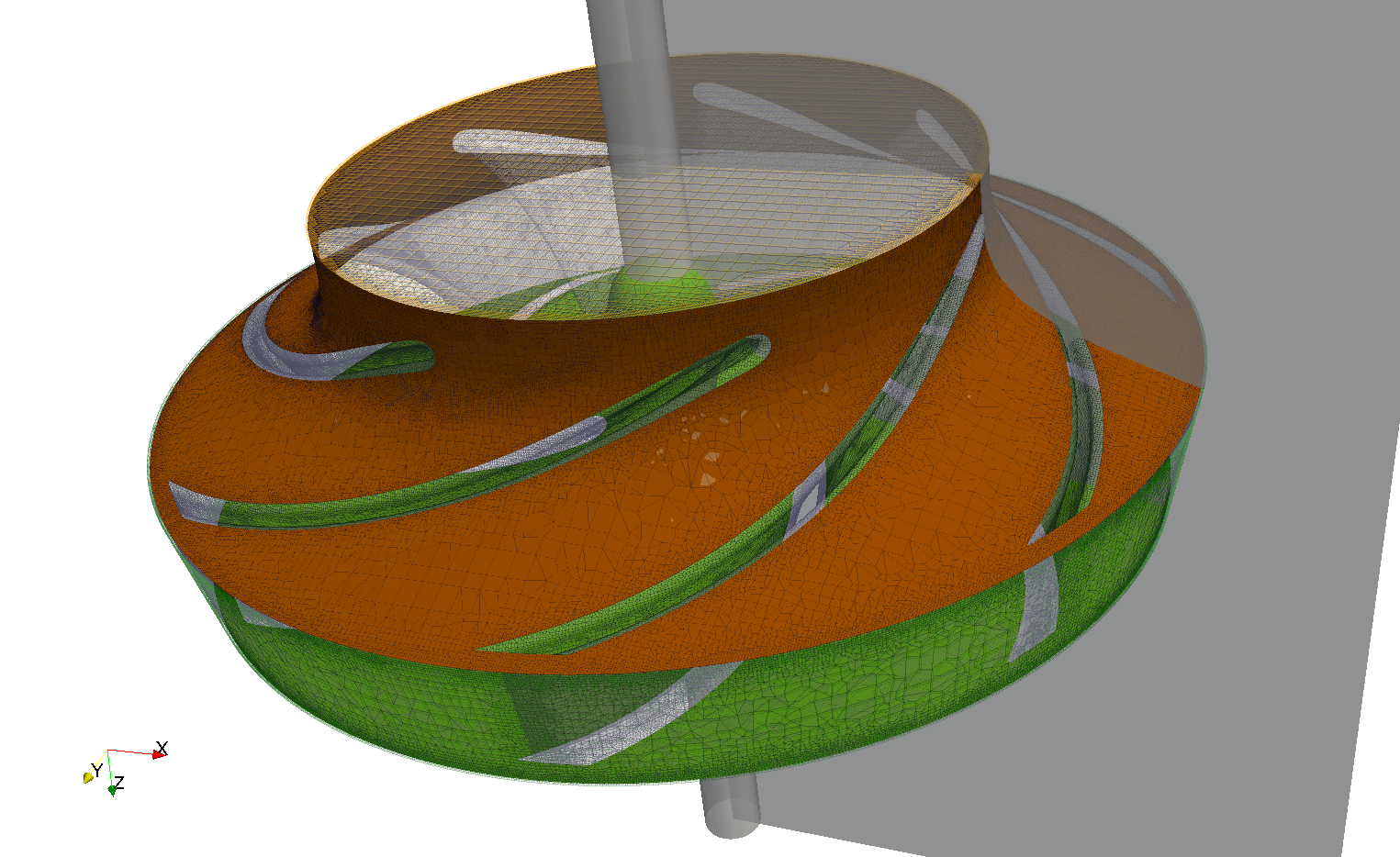
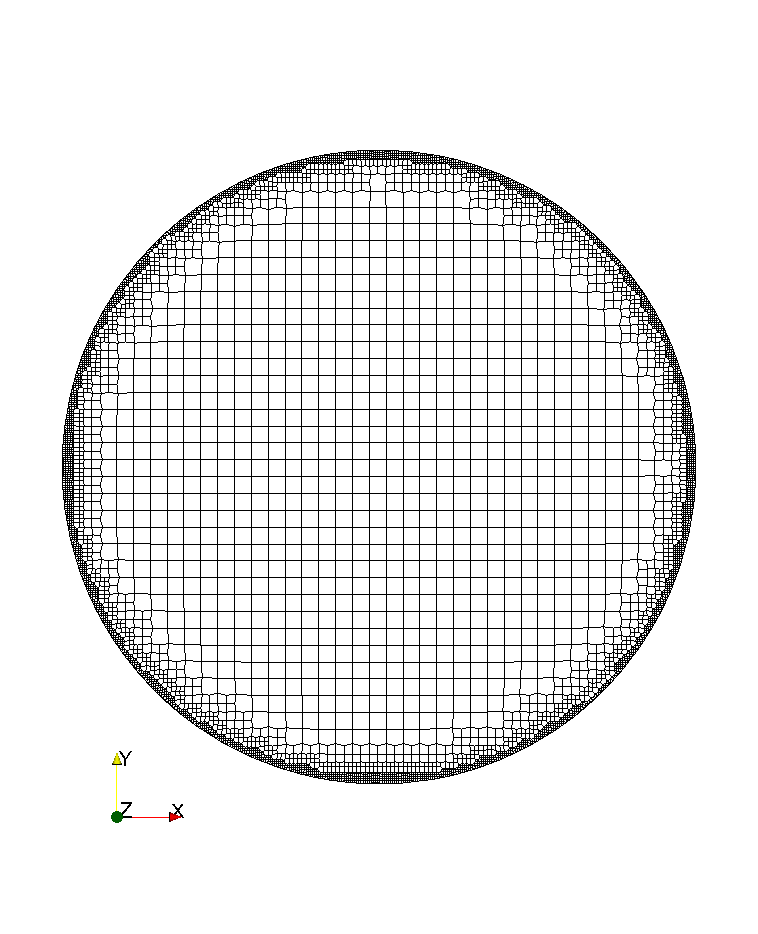

 , the normalized circular coordinate is transformed to
, the normalized circular coordinate is transformed to  and the remaining coordinate that is orthogonal to both, “along the stream”, is mapped to
and the remaining coordinate that is orthogonal to both, “along the stream”, is mapped to