Previous: cyclone-Euler case Up: Case structure Next: Initial and boundary condition
This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.
Initial and boundary condition for twoPhaseEulerFoam
- The directory 0.euler contains the definition of initial and boundary condition for each variable.
- The list of all variables contains Table
 .
. - Basic setup of initial and boundary condition:
- alphat.* – Set as calculated; At walls for continuous phase a standard wall function is applied.
- alpha.particles – Initial value: uniform 0; Inlet value: uniform 0.05.
- alpha.water – Initial value: uniform 1; Inlet value: uniform 0.95.
- epsilon.water – Initial and inlet value: uniform 3.144.
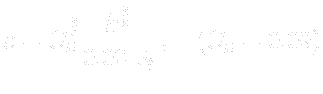
- k.water – Initial and inlet value: uniform 0.375.
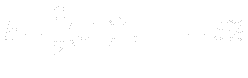
- nut.* – Set as calculated; At walls for continuous phase a standard wall function is applied.
- p – Set as calculated; Computed from p_rgh.
- p_rgh – Pressure value
 is set at the outlet.
is set at the outlet. - Theta.particles – Small value
 is set at the inlet.
is set at the inlet. - T.* – Initial and inlet temperature is set to
 K.
K. - U.* –
 m/s is set at the inlet (direction perpendicular to the inlet face).
m/s is set at the inlet (direction perpendicular to the inlet face).
Table: Initial and boundary conditions for twoPhaseEulerFoam.
|
|
|
|
|
<#37075#> |
|
|
|
|
|
<#37078#> |
|
|
|
|
|
<#37081#> |
|
|
|
|
|
|
|
|
|
|
|
- static pressure |
|
|
-
|
|
|
- granular temperature |
|
|
<#37092#> |
|
|
|
|
|
<#37095#> |
|
|